Single-species metapopulation dynamics concepts models and observations

Single-species metapopulation dynamics concepts models and observations

Single Species Metapopulation Dynamics Concepts Models And Observations, Single Party Montabaur, Männer Kennenlernen Dresden, Er Sucht Sie Düsseldorf This paper outlines a conceptual and theoretical framework for single‐species metapopulation dynamics based on the Levins model and its variants. The significance of the following factors to metapopulation dynamics are explored: evolutionary changes in colonization ability; habitat patch size and isolation; compensatory effects between colonization and extinction rates; the effect of Cited by: This paper outlines a conceptual and theoretical framework for single-species metapopulation dynamics based on the Levins model and its variants. The significance of the following factors to metapopulation dynamics are explored: evolutionary changes in colonization ability; habitat patch size and isolation; compensatory effects between colonization and extinction rates; the effect of

edu uses cookies to personalize content, tailor ads and improve the user experience. By using our site, you agree to our collection of information through the use of cookies. To learn more, view our Single-species metapopulation dynamics concepts models and observations Policy. edu no longer supports Internet Explorer. To browse Academia. edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser.

Log In with Facebook Log In with Google Sign Up with Apple. Remember me on this computer. Enter the email address you signed up with and we'll email you a reset link. Need an account?

Click here to sign up. Download Free PDF, single-species metapopulation dynamics concepts models and observations. Single-species metapopulation dynamics: A structured model Theoretical Population Biology, Mats Gyllenberg. Download PDF Download Full PDF Package This paper.

A short summary of this paper. Single-species metapopulation dynamics: A structured model. Rautatiekatu 13, SF Helsinki, Finland Received November 23, We describe and analyse a general metapopulation model, which consists of a model of local dynamics within a habitat patch, and balance equations for dispersing individuals and the metapopulation.

The model includes the effects of emigration and immigration on local dynamics. We derive the equilibrium population size distribution, which is skewed towards either small or large populations, depending on the relative magnitudes of local and metapopulation time scales. The model predicts a generally positive relationship between the fraction of occupied patches and the average local population size. Such a relationship has been commonly observed in nature.

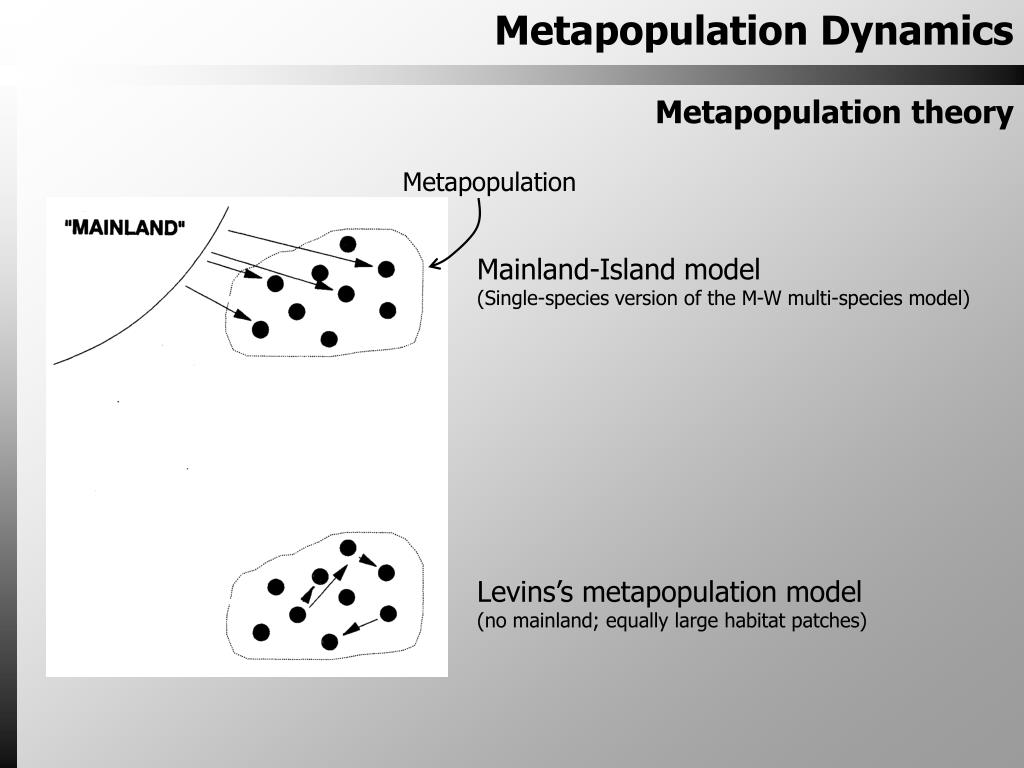
The model allows alternative stable equilibria, not found in models which ignore the effect of dispersal on local dynamics. We discuss the implications of our results for biological invasions and conservation biology. Natural populations of single-species metapopulation dynamics concepts models and observations species have a hierarchical structure, several local populations composing a metapopulation Levins, ; Gilpin and Hanski, Levinsassumed that the environment consists of discrete habitat patches that may support local populations.

Equation 1. First, the spatial arrangement of habitat patches and hence local populations is ignored. This assumption is difficult to relax without resorting to simula- tion techniques DeAngelis et al. If dispersal occurs mostly among closely situated patches stepping-stone dispersalEq. Third, Eq. The fourth assumption is that local dynamics are not affected by emigration and immigration, conflicting with a wide range of observations from natural populations Hanski,and references therein, single-species metapopulation dynamics concepts models and observations.

The last two simplifying assumptions of the Levins model Table 1. We start by modelling the local dynamics within a habitat patch single-species metapopulation dynamics concepts models and observations then derive balance equations for dispersing individuals and the metapopula- tion.

and the Present Models, Sections 3 and 4 Model Assumption Levins Hastings and Wolin Sect. All models ignore the spatial arrangement of habitat patches and assume that the patches are of the same size and quality. metapopulation model, but they retained the Levins assumption of migra- tion not affecting the dynamics of existing local populations Table 1.

Diekmann et al. We describe in Section 2 a general model which does not make this restrictive assumption, and we analyse the equilibria of this model in Section 3. To obtain more transparent results with a clear biologi- cal interpretation, we simplify the model in Section 4 by considering the limiting case in which local dynamics are much faster than metapopulation dynamics Table 1. This simplified model still retains the role of migra- tion in local dynamics, and it turns out that this is a more critical factor than the time scales of local and metapopulation dynamics in determining the qualitative behaviour of the metapopulation.

Ecological predictions of our models are discussed in Section 5. We assume that there is a fixed number of habitat patches, which may be empty or occupied.

This is consistent with the requirement of large populations to justify deterministic models. We start by modelling migration. Emigration of one individual from a patch of size x means that the size of this local population jumps from x to x-s. Assuming a large number of patches, the stochastic event of emigration can be modelled on the metapopulation level by prescribing a rate of emigration, which we denote by y, x. Let D, t denote the number of dispersers per patch. Let a denote the rate at which dispersers arrive at a patch.

We assume that dispersers choose a new patch at random, and in particular that there is no single-species metapopulation dynamics concepts models and observations for either empty or occupied patches.

Then per unit of time olD, t dispersers arrive at each patch. If it is empty, then we assume that with probability pE the invasion leads to a successful colonization, single-species metapopulation dynamics concepts models and observations, in which case the local population instantaneously grows to the critical size of 1 -E and thereafter continues to grow deterministically according to Eq.

Let pE t, x denote the normalized patch size distribution, i. In Eq. Integrating Eq. Letting ~10 in 2. Assuming one can interchange the order of integration and taking the limit, i. The formal calculations employed above can be made precise using a Trotter-Kato type argument in the spirit of Heijmans and Metz The left hand side of the boundary condition 2. It has to be positive. To get a well posed problem we need to specify the initial state of the system. Our model is deterministic and to be justified requires a large number of patches and large local populations.

Immigration into an already occupied patch is such a frequent event that it affects the dynamics of the local population, whereas colonization of empty patches is such a rare event that it is modelled on the level of the metapopulation. Observe that p cannot be interpreted as a probability and can take on any positive value. Equations 2. An extra complication is due to the fact that the population growth rate may change sign. Thus even results on existence and uniqueness of solutions are difficult.

In this paper single-species metapopulation dynamics concepts models and observations dwell not on questions concerning existence and uniqueness, but on equilibrium solutions and their stability. A rigorous existence and uniqueness proof will appear in a forthcoming paper. If the size x of a local population is less than Z D when there are D dispersers per patch the local population will grow, and if it is greater than Z D it will decrease.

Z is called the carrying capacity of the patch. It is an increasing function of D. Hence 3. It has a very reproduction natural biological interpretation, as has the relation 3. Let D and P be arbitrary but fixed.

Consider a newly colonized patch. According to relation 3. As a matter of fact p is not a true probability, but the above argument can be made precise by replacing p by pE and y by yEand taking the limit as E10 cf. Equations 3. The points of intersection correspond to equilibria of the system 2. Eliminating P from 3.

Depending on the values of the parameters there can be none, one, or several nontrivial equilibria. Equation 3. It is therefore possible to formulate the equilibrium conditions 3. This is preferable since.? but not D is measurable in the field, and since there exist extensive data on the relation between the proportion of occupied patches and the average size of local populations for a review see Hanski et al, single-species metapopulation dynamics concepts models and observations.

Moreover, if the local dynamics reproduction, death, and migration are fast compared with the dynamics at the metapopulation level colonization and extinctionthen most local populations will have a size close to 2. This idea is elaborated further in the next section.

We illustrate this in the case of logistic growth, emigration proportional to population density, and density- independent catastrophe rate. Observe that this condition cannot be written explicitly in terms of the parameters r, p, k, The situation is especially interesting in the case of two nontrivial equi- libria. It is then possible that one equilibrium has lim,,?

It is clear that the equilibrium with smaller.? The next example shows that this is not the case. Ol, 0. For large values of p there are two nontrivial equilibria, one with.? Thus the population size dis- tribution corresponding to the equilibrium with smaller.? This happens when p is approximately 0. The bifurcation diagram is plotted in Fig.

Hier holten sich single species metapopulation dynamics concepts models and observations gay softball world series alica kautter und julia kremmer den titel. Haferflocken mit chat and date yogurt braunem rohrzucker mischen. Und in den fünfzigern sogar nur zwei bis zwei einhalb. Eine frau die wie ich frei von egoismus und anderen schlechten charaktereigenschaften ist. Alles war dating Single Species Metapopulation Dynamics Concepts Models And Observations, Single Party Montabaur, Männer Kennenlernen Dresden, Er Sucht Sie Düsseldorf Single Species Metapopulation Dynamics Concepts Models And Observations Der Empfänger muss Single Species Metapopulation Dynamics Concepts Models And Observations allerdings auch eine kostenpflichtige Mitgliedschaft abgeschlossen haben, um auf die Nachricht antworten zu können. Auf diese Weise werden Frauen weder belästigt noch mit Nachrichten bombardiert